Dạ Trạch
Từ tính của các ô-xít và một số vật liệu có điện tử tương đối định xứ tại nguyên tử hoặc ion (thường là phản sắt từ) được giải thích bằng tương tác siêu trao đổi và tương tác trao đổi Heisenberg. Đó là hệ quả của nguyên lí loại trừ Pauli đặc biệt là bản chất phản đối xứng của hàm sóng của điện tử. Tương tác điện tử-điện tử tại các vị trí khác nhau có tồn tại trong các ô-xít nhưng thường là yếu.
Bài này chúng ta nghiên cứu về tính chất từ của kim loại, đó là những hệ trong đó điện tử từ hai hay nhiều vị trí khác nhau có thể cùng chiếm một liên kết cộng hóa trị hay liên kết kim loại. Đối với kim loại chuyển tiếp chúng ta gặp khó khăn vì các điện tử d trong các kim loại này không hẳn là định xứ mà cũng không hẳn là linh động. Đôi lúc chúng thể hiện như là các điện tử tự do nhưng đôi lúc lại thể hiện như là các điện tử định xứ. Mặc dù tương tác Heisenberg được áp dụng cho các điện tử định xứ với tương tác trao đổi yếu nhưng mô hình đó vẫn thường được áp dụng để mô tả tính chất sắt từ (J âm) và phản sắt từ (J dương) trong các kim loại. Trên thực tế, tương tác trao đổi trong kim loại phức tạp hơn nhiều. Thường thì tương tác trao đổi được đưa vào như là các số hạng bổ chính trong tính toán cấu trúc vùng năng lượng. Trước hết ta hãy bắt đầu bằng các dữ kiện thực nghiệm.
ĐƯỜNG CONG SLATER-PAULING
Từ tính của các ô-xít và một số vật liệu có điện tử tương đối định xứ tại nguyên tử hoặc ion (thường là phản sắt từ) được giải thích bằng tương tác siêu trao đổi và tương tác trao đổi Heisenberg. Đó là hệ quả của nguyên lí loại trừ Pauli đặc biệt là bản chất phản đối xứng của hàm sóng của điện tử. Tương tác điện tử-điện tử tại các vị trí khác nhau có tồn tại trong các ô-xít nhưng thường là yếu.
Bài này chúng ta nghiên cứu về tính chất từ của kim loại, đó là những hệ trong đó điện tử từ hai hay nhiều vị trí khác nhau có thể cùng chiếm một liên kết cộng hóa trị hay liên kết kim loại. Đối với kim loại chuyển tiếp chúng ta gặp khó khăn vì các điện tử d trong các kim loại này không hẳn là định xứ mà cũng không hẳn là linh động. Đôi lúc chúng thể hiện như là các điện tử tự do nhưng đôi lúc lại thể hiện như là các điện tử định xứ. Mặc dù tương tác Heisenberg được áp dụng cho các điện tử định xứ với tương tác trao đổi yếu nhưng mô hình đó vẫn thường được áp dụng để mô tả tính chất sắt từ (J âm) và phản sắt từ (J dương) trong các kim loại. Trên thực tế, tương tác trao đổi trong kim loại phức tạp hơn nhiều. Thường thì tương tác trao đổi được đưa vào như là các số hạng bổ chính trong tính toán cấu trúc vùng năng lượng. Trước hết ta hãy bắt đầu bằng các dữ kiện thực nghiệm.
ĐƯỜNG CONG SLATER-PAULING
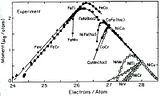
Đường cong Slater-Pauling cho thấy mô men từ (đơn vị là mB) đối với các hợp kim là một hàm của mật độ điện tử hóa trị hay thành phần hợp kim.
Mô men từ trung bình trên một nguyên tử sắt, cô-ban và ni-ken lần lượt là 2.2, 1.7 và 0.6 mB. Hình 1 cho thấy mô men từ của một số hợp kim, ta thấy rõ ràng mô men từ phụ thuộc vào số điện tử trung bình trên một nguyên tử. Lấy ví dụ Co có số nguyên tử là Z=27 và hợp kim Fe50Ni50 cũng có số nguyên tử trung bình Z=27, và chúng có mô men từ trên một nguyên tử bằng nhau. Giá trị mô men đạt cực đại khoảng 2.5 mB với Z=26.5 điện tử/nguyên tử đối với hợp kim có cấu trúc BCC như là FeNi, FeCr.
Mô men từ của các kim loại và hợp kim trên có thể tính toán chính xác từ cấu trúc vùng năng lượng. Nhưng trước hết ta phải xem xét ba khái niệm:
1. Hình 2 cho minh họa sự mở rộng của các mức năng lượng (trường hợp này là các trạng thái 4s và 3d) khi khoảng cách giữa các nguyên tử giảm đi. Chú í rằng trạng thái 4s (l=0) nằm gần hạt nhân hơn trạng thái 3d (l!=0) nhưng trạng thái 4s lại mở rộng hơn trạng thái 3d nên chúng có xu hướng tương tác với các nguyên tử lân cận tại các khoảng cách xa hơn. Các trạng thái nằm ở dưới vùng đang xem xét là các trạng thái liên kết có hàm sóng đạt cực đại tại khoảng giữa các nguyên tử trong khi các trạng thái nằm trên vùng đang xét là các trạng thái phản liên kết với hàm sóng có giá trị thấp ở khoảng giữa các nguyên tử. Hình 2 cho thấy vùng điện tử gần tự do s trải rất rộng và theo hàm E1/2 còn vùng d có mật độ trạng thái cao hơn và trải hẹp. Diện tích của vùng s so với d là 2:10. Với mức Fermi như hình vẽ thì nếu mức Fermi thay đổi sẽ làm thay đổi diện tích của vùng d nhiều hơn vùng s. Đây chính là nguyên nhân quan trọng làm cho tính chất từ chủ yếu phụ thuộc vào trạng thái d.

(Hình 2)
1. Hình 2 cho minh họa sự mở rộng của các mức năng lượng (trường hợp này là các trạng thái 4s và 3d) khi khoảng cách giữa các nguyên tử giảm đi. Chú í rằng trạng thái 4s (l=0) nằm gần hạt nhân hơn trạng thái 3d (l!=0) nhưng trạng thái 4s lại mở rộng hơn trạng thái 3d nên chúng có xu hướng tương tác với các nguyên tử lân cận tại các khoảng cách xa hơn. Các trạng thái nằm ở dưới vùng đang xem xét là các trạng thái liên kết có hàm sóng đạt cực đại tại khoảng giữa các nguyên tử trong khi các trạng thái nằm trên vùng đang xét là các trạng thái phản liên kết với hàm sóng có giá trị thấp ở khoảng giữa các nguyên tử. Hình 2 cho thấy vùng điện tử gần tự do s trải rất rộng và theo hàm E1/2 còn vùng d có mật độ trạng thái cao hơn và trải hẹp. Diện tích của vùng s so với d là 2:10. Với mức Fermi như hình vẽ thì nếu mức Fermi thay đổi sẽ làm thay đổi diện tích của vùng d nhiều hơn vùng s. Đây chính là nguyên nhân quan trọng làm cho tính chất từ chủ yếu phụ thuộc vào trạng thái d.

(Hình 2)
(a) Sự biến đổi của trạng thái 4s và 5d theo khoảng cách giữa các nguyên tử; (b) mật độ trạng thái 4s và 3d của các điện tử có spin thuận và nghịch bị dịch khỏi nhau.
2. Lí thuyết Weiss về sắt từ giả thiết có một trường hiệu dụng nội tại HE=lM. Cơ học lượng tử cho thấy đó là do tương tác Culomb tạo nên trong các hệ có hàm sóng tuân theo nguyên lí loại trừ Pauli. Trường hiệu dụng này gây ra một dịch chuyển giữa vùng có spin thuận và spin nghịch của vùng d (hình 2b). Còn vùng s gần như tự do nên sự dịch chuyển là rất nhỏ làm cho số điện tử s có spin thuận và nghịch gần như bằng nhau. Theo qui tắc Hund thứ nhất thì trước tiên các điện tử sẽ lấp đầy các trạng thái suy biến với các spin sắp xếp song song với nhau, điều này làm giảm lực đẩy Culomb giữa các điện tử có cùng điện tích âm vì chúng chiếm các trạng thái quỹ đạo có độ phủ vùng theo không gian nhỏ nhất. Nhưng đối với các trạng thái không bị suy biến, để có thể đặt điện tử vào các trạng thái không bị suy biến đó nhằm thỏa mãn quy tắc Hund thì phải cần thêm một năng lượng, năng lượng này sẽ lớn nếu trạng thái đó trải rộng trong không gian (tương đương với mật độ trạng thái Z(E) nhỏ). Sự cạnh tranh giữa việc tiết kiệm năng lượng trao đổi và chi phí cho động năng được biểu diễn bằng tiêu chuẩn Stoner cho một hệ có tính sắt từ:
J(EF) Z(EF) > 1 (1)
Một hệ có tính sắt từ mạnh nếu hệ đó có tích phân trao đổi và mật độ trạng thái cao tại mức Fermi.
3. Cần lưu í rằng các trạng thái liên kết giữa các nguyên tử sẽ ưu tiên các cặp spin phản song song với nhau, ngược lại, các trạng thái phản liên kết ưu tiên các cặp spin song song với nhau. Đó là một trong những lí do làm cho các nguyên tố nữa đầu dãy kim loại chuyển tiếp – V, Cr, Mn (EF nằm trong phần liên kết của vùng d) có tính phản sắt từ và các nguyên tố ở nửa cuối dãy – Fe, Co, Ni (EF nằm trong phần liên kết của vùng d) có tính sắt từ.
(Còn nữa)